ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОЙ ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТИ ПО КРИТЕРИЮ МИНИМУМА РИСКА
В рассмотренных выше задачах определения достоверности статистических оценок с помощью доверительных интервалов предполагалось всегда известным значение доверительной вероятности y(Yi» Тг)- На практике выбор этого значения всегда представляет определенные трудности. Наиболее употребительны выбранные округленно с точностью до 0,010 и 0,005 следующие значения у: 0,995; 0,990; 0,975; 0,950; 0,925; 0,900 ; 0,800; 0,700; 0,500. В некоторых руководящих документах директивно задаются значения доверительной вероятности, иногда ее задают так, чтобы соответствующие квантили нормального распределения щ1 и и1+1 могли быть
~2
округлены до целых или десятых долей (например, Ы1+т = 3 и у =
~2~
= 0,9973). Иногда выбирают квантили нормального распределения, соответствующие целым значениям срединных отклонений
Ех — рах]/л2 да 0,6744о* (например, при Ех — 4 имеем ы1+ = 2,698 да
~
« 2,7 0,993). Чаще всего величину у принимают такой, для
которой имеются соответствующие таблицы.
Используя положения теории статистических решений, основные результаты которой изложены в ряде работ [27, 68, 691, можно найти оптимальную в некотором смысле величину у. Рассмотрим решение
Л
такой задачи. Пусть найдена оценка 0Х параметра ©х и известна (или
Л, ,
оценена) ее дисперсия о210ж] = о,:1, причем метод нахождения величин
Л
0Х и ое не накладывает ограничений на решаемую задачу. Будем по-
Л л
лагать, что задан закон распределения оценки вх с плотностью /в (©*). В терминах теории статистических решений интерес представляет
л
правило принятия оптимального в некотором смысле решения ©жР, характеризующего положение истинного значения неизвестного 0Х. В рассмотренных выше задачах таким решением служили случайные
л л
односторонние нижний ©Х1Н или верхний ©*,в доверительные пределы. В данной задаче выбрана элементарная решающая функция
Если будет найдено оптимальное значение Д0яР, то будет определено и правило принятия решения.
Заметим, что при известном законе распределения оценки с плот-
л
ностью вероятности /н (©ж) существует однозначное соответствие между величиной А©жр и соответствующими доверительными вероятностями Yip или угр:
^*+Лв*р
J ме*)Ас = ър; (5-142)
—оэ
«,г-Дв:.Р
J fe(e Jrfe«=l-Yip. (5.143)
—оо
Для определения величины Д0К (индекс «р» будем относить только к оптимальному значению параметра Д0Х) введем случайную величину
л
I/ = [(©ж — Д©ж) — ©жі/oe и построим функцию потерь оi(y), вызываемых возможными ошибками в определении истинного значения л л
©ж по его оценке ©ж — Будем полагать, что в точке у — 0 (0Х = ©ж — — Д©ж) потери равны нулю. С увеличением величины у, т. е. когда л
©ж — Д@ж больше истинного значения, возникают потери, связанные с тем, что за истинную характеристику ©х принимаем более высокое
л
значение ©ж — Д©ж. При у<_ 0 потери связаны с занижением неиз
вестного истинного значения. Обычно потери //> 0 и уС 0 неодинаковы, т. е. функция потерь to (у) несимметрична относительно нуля.
Например, если ft., — обобщенный показатель надежности группы ЛК, то при /,/> 0 потери будут связаны с невыполнением некоторыми ЛА поставленных задач, так как истинная надежность окажется меньше предполагаемой. При у С 0 потери могут быть значительно меньше, так как в этом случае часть ЛК или ЛА окажутся лишними, ненужными для выполнения заранее спланированных задач. В рассматриваемом примере при у<~_ 0 теряем стоимость лишних ЛК, а при у> 0 — стоимость невыполнения поставленных перед группой ЛК задач.
Таким образом, функция потерь в общем виде может быть задана следующим образом:
|
о, (//) = / “l(^ При У^ °’ 1 ®2(у) при у<0. |
(5.144) |
|
Наиболе е простые функции потерь описываются ратическими или показательными функциями: |
линейными, квад- |
|
„,(„) ( Ау ПР" У > 0- 1 — В у при у <0; |
(5.145) |
|
[Аф при у Ss — 0, [В if при ус 0; |
(5.146) |
|
| А (1 — е~У) при у с 0, М{У)-[В(1— е>) при г/< 0, |
(5.147) |
где А и В — постоянные коэффициенты.
л
Случайная величина у = ((0,,. — Aft.,) — ©J/сге имеет определенный закон распределения с плотностью вероятности fy (у), которую
л
нетрудно найти, зная плотность /я (ft,). Так как у является линейной,
л
а следовательно, и монотонної! функцией от 0Г, то в соответствии с известными правилами (см. [12, 531) нахождения закона распределения монотонной функции от случайного аргумента имеем
|
А |
Л |
|
|
©ж= а, у + Д0* + ©*; |
ау |
|
|
fv (у) = | | U (ачУ і д0 |
X +©:,) = ай /© ( а®У + Д0.г +©д) • |
|
(5.148) |
|
-(і’+Лв*)2/* |
|
/2* |
то в соответствии с (5.148) получим
где Де=Д0ж/ов.
Плотность fy(y) характеризует вероятность появления тех или
Л
ИНЫХ отклонений </=[(0т—Д0ж)—0Ж] /а», что позволяет найти функцию риска
оо
Г {у, Д0Ж) = Л4 fill (у) = [ О) (у) fy (у) dy, (5.150)
—оо
которая по определению является математическим ожиданием функции потерь. л
Нетрудно заметить, что функция риска будет зависеть от искомой величины Д0Ж.
Введем критерий оптимальности принятого решения, за которой примем минимум функции риска, т. е. будем считать оптимальной такую величину Д0лр, при которой функция (5.150) минимальна: г(у, Авхр) = min.
Рассмотрим решение задачи для наиболее интересных случаев, когда
Л
оценка 0Э. имеет нормальное распределение, а функция потерь задана в виде (5.145) — (5.147).
При показательной функции потерь (5.147) в соответствии с (5.149) и (5.150) имеем
О
г(у, Авх)= SB(l-e*)~Lr-e 2 dy + A(l-e-^-L — х
J Vїї J V2n
|
Ц! 2* L-i |
|
(1— ey)e (* + 48*)® |
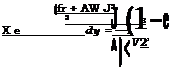 |
|
— DO U
где A—A/B.
Для определения минимума функции (5.151) достаточно минимизировать выражение в квадратных скобках, которое зависит от оптимизируемого параметра Д©ж и величины Л.
Таким образом, оптимальное решение полностью определяется только масштабом потерь (масштабным коэффициентом А) слева и справа
Постоянный множитель В! 2л в выражениях (5.151)—(5.153) не меняет положения минимума функции риска, поэтому в дальнейшем
 будем его принимать равным единице.
будем его принимать равным единице.
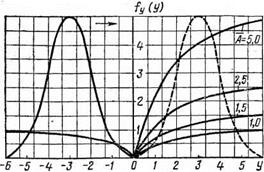
Дадим геометрическую интерпретацию решения задачи. Для случая, когда функция потерь задана в виде (5.147) и закон распре — л
деления оценки &х нормальный, вид функций ы(у) и fy (у) представлен на рис. 5.6. Для определения функции рис — Рис. 5.6. Построение функции риска ка необходимо интегри
 |
ровать произведение <й(у) fyiy) при различ
|
г(ЛЄх)
|
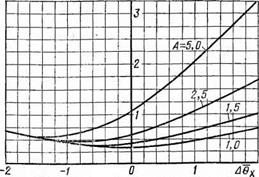
Xfy(y) был бы минимальным. Г, р На рис. 5.7 даны графики функции относительного риска, полученные для условий рис. 5.6, а на рис.5.8 — за — 0,7 висимость оптимальной доверительной вероятности Yip от масштабного коэффициента A D5 (кривая 1). Заметим, что ’ функция Yip (А) практически
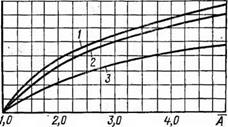 линейна при-Л > 2,5 И может Рис — 5-8- Оптимальная доверительная ве — — г роятность при различных функциях потерь
линейна при-Л > 2,5 И может Рис — 5-8- Оптимальная доверительная ве — — г роятность при различных функциях потерь
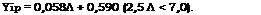
 быть аппроксимирована выражением
быть аппроксимирована выражением
Для случая линейной функции потерь в выражении (5.152) можно свести интегралы к табличным, при этом упрощается поиск минимума функции:
0 _ (»+A©2) °° (p+Aty)2
Г(д©*) = — j уе 2 dy + A^ye 2 dy.
■—со О
Введем замену переменных t = у + Двх, получим
![]() Д©
Д©
r(/�T)= — ^ (t — Д0Ж) е dt -{- Л (t Д0лс)е dt —
|
ДЄ ______ L /2 Дв ___________________ !— /2 V 2 * __ 2 te dt + Г Д©хе dt + А te |
|
dz + Д©*1 А2к — In — і -І |
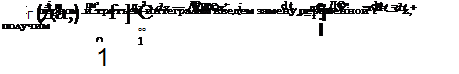 |
де
|
—У^к Ф<) (А©*) |
|
|
|
|
|
|
ДЄ*
-Т^ _
|
-4л е* |
|
1 I —2 е— Тди* (см. табл. П. 1). |
4 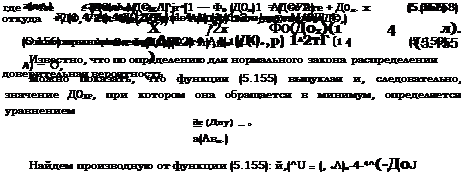
ЛЛ0жК 2* [1 — Ф0 (А0Х)]= є +Д0Х j/йГ Ф0 (Д© J 4
В соответствии с (5.159) и (5.160) для случая линейной функции потерь (5.145) окончательно получим очень простое выражение для оптимальной по критерию минимума риска доверительной вероятности одностороннего доверительного интервала:
Yip — Л/(1 — f — Л) . (5.161)
Вид этой зависимости представлен на рис. 5.8 кривой 2. Аналогично можно решить задачу и для случая нелинейной несимметричной функции потерь вида (5.146). Введя новую переменную t = у + Д©ж, проинтегрируем функцию (5.153) при В! 2п = 1 и получим
Лв* _ —4-<z _г _ — 4-
г (Д0Л) = Г (f— А©т)2е di + A I {t —Л0Х)2 е dt
 |
-І
(5.162)
Обозначим в (5.162) первый интеграл /ь четвертый J4 и проинтегри-
руем их по частям при и = t, v = •—е и dv = te dt.
|
Л0А* -~-*2 |
|
__ 2 _______________________ __ A0;ve + 1а2тг Фп(Д0*) ; |
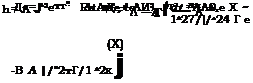 |
|
Получим:
+ А г2к [1 — Ф0 (А©ж)1,
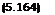 так как, раскрывая по правилу Лопиталя неопределенность /е = —<г
так как, раскрывая по правилу Лопиталя неопределенность /е = —<г
= tie2 при t = оо, получим выражение, равное нулю.
Второй интеграл в (5.162) /2, пятый /5 могут быть взяты при /2 = г:
|
4-* |
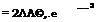
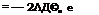 (5.166)
(5.166)
Третий интеграл в (5.162) J3, шестой Л — табличные:
г ле* — — />
/3 = Д©2 f е d/ = ]/2ЇсА©І —f е dt =
* -L /а* -L
|
-4-*1 |
= ]/2jc ЛД0ІІ1 — Ф0 (А0г)]. (5.168)
Суммируя (5.163)—(5.168), получим
_ — _ -4й**
г (Д©д.) = — А ©де + У 2п Ф0 (А0л;) -Т 2А©л;Є — Т
_ _ — Т_ де2 __ _
+ V2я А©* Ф0 (А©*) +ЛД©д е + А Іл2п 11 — Ф0( Д©*)1 —
+ ] ^тгЛД©! [ 1 — Ф0 (Д©,)] = Д0* е + ЦЪ Ф0 (Д©*) + Кйс Д©*Ф0 (Д©,) + А У 2т — — А |/2л Ф0 (Д©*) + /2к Ш1 — ^ ГЪ- ЛД@| Ф0 (Д©*)
![]()
![]()
![]() = Д©хе (1 — А) 4- г2т Ф0 (Д ©*) (l — A) — f-
= Д©хе (1 — А) 4- г2т Ф0 (Д ©*) (l — A) — f-
+ У ml ф0(Д©*) (і — л) + Я|/ас(і + Дві).
|
г (Дв*) = А! 2я (1 — f-A©*) + (1 — А) |
|
) г2п Ф0(А©*)4- (5.169) |
Окончательно имеем
Функция (5.169) выпуклая, поэтому искомый ее минимум определяется решением уравнения (5.156).
|
дг = 2Д©Л. Л llh + (1 — Л) I е |
|
-±л*2Х 2 х |
|
4- А©* є |
|
] — 2Д©Ж А ]^2п -}-2(1 — Л) [ V 1/Т2«Дв*Фо(Де*)] • |
|
— —де* 2 * |
![]()
В соответствии с (5.169) получим
На основании (5.170) уравнение (5.156) после умножения на постоянную величину 1/2; 2я можно записать в виде
Заметим, что при Л = 1 получаем оптимальное решение Д0жР = = 0, что и следовало ожидать, так как при симметричной функции
л
потерь оптимальна несмещенная оценка ©ж. Уравнение (5.171) трансцендентное, но его решение может быть легко найдено графически с использованием табличных функций.
Введя обозначения Д0жР = дг, в соответствии с (5.171) имеем
гдef(x) находим по табл. П.2; Ф0(л:) — по табл. 1X3. Результаты решения уравнения (5.172) и вычисления функции Фо(А0ХІІ) = уір(-А) представлены кривой 3 на рис. 5.8.
Теоретически интересен случай, когда функция потерь имеет вид
|
-І Vz* ~~ дїї |
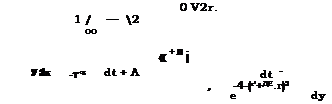 |
|
т. е. потерн постоянны и не зависят от величины ошибки в определении истинного значения. При этом функция риска
= В [Ф0(Авх) + Л — ЛФо(Д0*)] = В [А — (А — 1) Ф0 (Д©*)]. (5.174)
Минимум функции (5.174) достигается при А©* = + оо, если Л> 1, что соответствует Yip = 1.0.
Пример 5.25. Найти оптимальное по критерию минимума риска решение о неизвестном истинном значении R обобщенного показателя надежности ЛК,
А
если по результатам эксплуатации найдена несмещенная оценка R = 0,8000, имеющая нормальное распределение, а ее среднее квадратическое отклонение
Л
ст[/?] = 0 = 0,1000. Известно, что невыполнение задачи комплексом приводит
R
к потерям, в 10 раз большим стоимости самого ЛК-
В этих условиях будем считать, что функция потерь линейна и имеет вид
(5.145) при А = А/В — 10. Решающее правило (5.141) имеет форму R„ = R —
-А Яр.
В соответствии с (5.159) имеем Ф(А RJc ) = А/(А X 1) = 10/(10+ 1) «
Д
« 0,9091. По табл. П. З, интерполируя, находим Д Вр/0^« 1,335, откудаД/?р =
= 1,3350 = 1,335 • 0,100 = 0,1335.
R
Следовательно, оптимальное решение состоит в том, чтобы принять за истин-
А
ное значение R величину Rp = 0,8600 — 0,1335 = 0,7205.
Найденное оптимальное решение соответствует принятию за истинное зна-
А
чение R одностороннего нижнего доверительного предела RlH, найденного с доверительной вероятностью 0,9091.